West Nile Virus Spreads Through United States
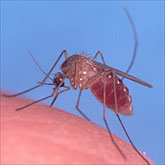 Viruses have been the scourge of humankind throughout history. Our most feared diseases, AIDS, smallpox, rabies and even the common cold, are all caused by viruses. Now, a dangerous Old World virus has made its first appearance in the United States. It is called the West Nile virus and it has been increasingly in the news, showing up first in New York City in 1999, and then rapidly spreading through the eastern United States. It is now poised to jump the Rockies and spread throughout the western United States and Alaska.
Viruses have been the scourge of humankind throughout history. Our most feared diseases, AIDS, smallpox, rabies and even the common cold, are all caused by viruses. Now, a dangerous Old World virus has made its first appearance in the United States. It is called the West Nile virus and it has been increasingly in the news, showing up first in New York City in 1999, and then rapidly spreading through the eastern United States. It is now poised to jump the Rockies and spread throughout the western United States and Alaska.
The virus belongs to a group of viruses called flaviviruses. Flaviviruses also cause Yellow fever and Dengue fever and are usually spread by mosquitoes. First discovered in Africa in the 1930s, it is prevalent throughout Africa, parts of Europe and Asia.
The great majority of cases of the West Nile virus in humans cause nothing more than flu-like symptoms. However, if the virus enters the brain or the spinal cord, it causes painful and potentially deadly inflammation. This is seen mostly in persons with compromised immune systems. The virus is not passed on by an infected person, however. Its mode of transmission is the mosquito and primarily the crow. When a mosquito bites a crow and one of them is infected, the uninfected one receives the virus and becomes a carrier. Currently there is no way to treat the virus, nor is there any vaccine. But keep in mind that although it can be deadly, fewer than 20 people in the US have succumbed to the virus. Scientists are working on a vaccine. Until then, the best advice: drain standing water, wear long sleeves, use an insect repellent, and stay indoors at dusk and dawn when mosquitoes feed.