The Doppler Effect
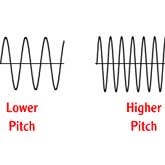As any object moves through the air, the air near the object is disturbed. The disturbances are transmitted through the air at a distinct speed called the speed of sound, because sound itself is just a sensation created in the human brain in response to small pressure fluctuations in the air. Sound moves through the air as a series of waves. When the waves pass our ears, a sound is detected. The distance between any two waves is called the wavelength and the time interval between waves passing is called the frequency. The wavelength and the frequency are related by the speed of sound; high frequency implies short wavelength and low frequency implies a long wavelength. The brain associates a certain musical pitch with each frequency; the higher the frequency, the higher the pitch. Similarly, shorter wavelengths produce higher pitches. The speed of transmission of the sound remains a constant regardless of the frequency or the wavelength.
The speed of sound only depends on the state of the air (or gas) medium, not on the characteristics of the generating source. Because the speed of sound depends only on the state of the gas, some interesting physical phenomena occur when a sound source moves through a uniform gas. You can study some of these phenomena by using the interactive sound wave simulator. As the source moves, it continues to generate sound waves which move at the speed of sound. Since the source is moving slower than the speed of sound, the waves move out away from the source. Upstream (in the direction of the motion), the waves bunch up and the wavelength decreases. Downstream, the waves spread out and the wavelength increases. The sound that our ear detects will change in pitch as the object passes. This change in pitch is called a doppler effect. There are equations that describe the doppler effect.
As the moving source approaches our ear, the wavelength is shorter, the frequency is higher and we hear a higher pitch. If we let (fa) be the approaching frequency, (a) be the speed of sound, (u) be the velocity of the approaching souce, and (f) be the frequency of the sound at the source, then fa = [f * a] / [a - u]. As the moving source leaves us, the wavelength is longer, the frequency is lower and the pitch is lower. Again. if (fl) is the leaving frequency, then fl = [f * a] / [a + u].
About the Author
NASA Glenn Research Center
The NASA Glenn Research Center in Cleveland, Ohio designs and develops innovative technology to advance NASA’s missions in aeronautics and space exploration.
